近似微分器

今日は近似微分器の話をしようと思います。

近似微分器とは、微分器にLPFを追加した者を言います。

設計方法は、s領域でLPFにsを掛け双一次変換（他にも方法はあるが）するか

z領域で作ったLPFに( (1-z^-1)/T) :離散微分器を掛けて作るかの２択でしょう。

まず、微分器とは　微分を意味します　。

直流成分は０に

sinwtはwcoswtに：つまりw倍に　という事です

微分器はsです。　s=jwの特性は

の通り、比例です。exp(jwt)->jw exp(jwt）のようにjw=w*exp(PI/2 *j)がかかるので,

PI/2だけ位相がずれます。wが負（高域）はwが負となるため -1＝exp(-PI*j)よりPIだけ位相が減ります。

離散化した 　　(1-z^-1)/T　　のＤＴＦＴ（z変換）の結果を見てみると

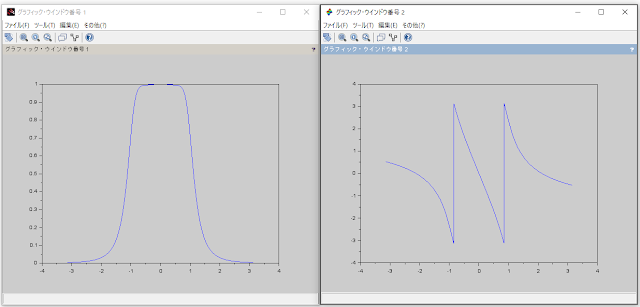
T=0.01;
function [F]=Hz(z);
    F=(1-(z^-1))/0.01;
endfunction
w1 = -1*%pi:2*%pi/1000:%pi;              //周波数軸
T = 0.01;                                //サンプリングタイム

for i = 1:1001
   //k = Hz(exp(%i*w1(1,i)));
   k = Hz(exp(%i*w1(1,i)*T));    //z = exp(j*w正規化*Tsamp)であるので
   //k = Hz(%i*w1(1,i));
   y(i)=abs( k );                         //振幅
   y2(i)=atan(imag(k),real(k));           //位相
end

//y(1001)=0;                              //グラフの軸をきれいにするため
figure(1);
plot(w1,y');

figure(2);
plot(w1,y2');

というプログラムで見ると       z=exp(%i*w1(1,i)*T)　としてプロット

s領域と差は見たところないです。ただ、 z=exp(%i*w1(1,i)*T)　　Ｔが付いています。

Scilabで行っています。

五次バタワースフィルタをLPFとします。

F=1/((z^5)+3.246*(z^4)+5.236*(z^3)+5.236*(z^2)+3.246*z+1);     //5次バタワースフィルタ

がs域でのフィルタです。（1Hzでカット）

周波数応答は

位相については-PI~PIに直線的に変動して居るのがわかります。

sを掛け微分器とした場合

F=z/((z^5)+3.246*(z^4)+5.236*(z^3)+5.236*(z^2)+3.246*z+1);     //5次バタワースフィルタ*微分器

とすると、（z = jw としてプロット）

バタワースのカットオフ1Hzまでは比例が現れ、それ以上の高周波ゲインが０になっていくのが現れています。位相特性はPI/2->-PI/2まで0<w<wcutの間で変化している。これは波形形状を悪化させるがバタワースフィルタを使っている以上どうしようもない。

z領域で設計したバタワースフィルタ:cutoff 1rad/sで設計したもの

双一次変換後:cutof 0.9272952rad Tsamp=0.01sで計算

                      2     3    4   5                 

                  1 + 5z + 10z + 10z + 5z + z                  

   ----------------------------------------------------------  

                            2          3          4         5  

   -6.5 + 52.548z - 177.224z + 321.192z - 312.276z + 154.26z   

に微分器　(1-z^-T)/T   :^-Tとなるのはz=exp(jw):とwを正規化周波数として扱うため

を掛けたもの

F=(1-z^(-1*T))/0.01* (1 + 5*z + 10*z^2 + 10*z^3 + 5*z^4 + z^5 )/(-6.5 + 52.548*z - 177.224*z^2 + 321.192*z^3 - 312.276*z^4 + 154.26*z^5   );  
   //5次バタワースフィルタ 微分器

をＤＴＦＴをすると

s領域と変わらない応答となっています。

問題としてはやはり位相特性がかなり悪化するでしょう。カットオフ周波数付近の高域の周波数では位相がＰＩほど遅れるので形状変化がはっきり出ます。

Tsamp = 0.01s　なら　0.5rad まで利用するなら （100Hz*(0.5/2PI) =8Hz 　 まで利用）位相はＰＩ／２ ずれ程度で許されるでしょう。

ＦＩＲを使えば波形を崩さずにできるでしょう。今度試します。

次に実際のシステムに適用して微分器の性能を見てみましょう。

動画のようなシステムで、振り子の先端に加速度ジャイロセンサ、根元に角度測定用エンコーダー（分解能1°）の二つを付けています。

エンコーダーの出力を微分し、ジャイロセンサの出力と比較し微分器の性能を比較します。

微分器は分解能の影響が大きく感じます。0vと１vしか取らずTsamp　＝　0.01　なら

(1-z^-1)/T という離散化微分器ならば 100[v/s]か0[v/s]しか取りません。Tsampの値が小さいほど、微分器の出力も敏感でかなりばたついた結果になります。

実際の実験結果は

青：ジャイロ　　赤:オイラー法による、エンコーダー微分

形状はかなり正しく、計算できているといえるでしょう。だた、やはり分解能の問題でばたついています。